Eratóstenes: Medida del radio de la tierra
Eratóstenes nació en Cirene en el año 276 a. C y se cree que era de origen caldeo. Fue matemático, astrónomo y geógrafo. Alrededor del año 255 a. C ,fue nombrado director de la Biblioteca de Alejandría por el rey Ptolomeo Evegetes. Trabajó con problemas de matemáticas, como la duplicación del cubo y los números primos. Hemos podido conocer algo de sus trabajos, merced a comentarios y citas de otros autores. Una de sus principales contribuciones a la ciencia y a la astronomía fue su trabajo sobre la medición de la Tierra, para hallar el radio de la tierra solo necesitó dos palos, una buena cabeza y mucha curiosidad. En esta práctica hemos intentado seguir su procedimiento lo mas fielmente posible, pero cn la ayuda de haber leido el libro anteriormente.

Procedimiento
Este ejercicio lo realizaremos sobre una superficie plana, ya que sin ella este ejercicio no se podria hacer, lo que hay que hacer es poner el papel en la dirección donde sale el sol y en donde se pone el sol (este- oeste). Colocaremos un gnomon, es decir una especie de obelisco y cada media hora tomaremos la medida de la sombra que proyecta. Observamos que a las 12 de la mañana es cuando el sol da una iluminacion mayor por lo tanto la sombra adquirirá el mayor tamaño posible, si seguimos avanzando en el tiempo veremos que despues del momento álcido de luz, el tamaño de la sombra disminuye poco a poco. Digamos que las distancias frente al tiempo dentro de una gráfica sería una parábola.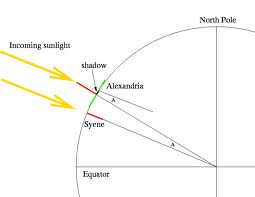
Para tomar como referencia dos puntos tomaremos Madrid y Jaén, la distancia entre ellas es de 335 km, en Madrid al mediodía el sol tenía un ángulo de 48´09 grados y en Jaén tenía un ángulo de 52 ´25grados. Lo que hizo eratostenes fue restar los dos angulos para poder hallar el ángulo que había entre las dos ciudades tomando como centro el centro de la tierra.
52´25-48´09= 4´16 grados entre las dos ciudades tomando como referencia el centro de la tierra.
El siguiente paso es medir el perímetro de la tierra para lo que utilizó una simple regla de tres.
Si en 4´16 grados la distancia es de 335 km en 360 grados la distancia sera x.
Perímetro=360x 335/4’16 = 32860´66 km es el radio de la tierra
Radio=32860´66/ 2x3,14 = 5318´93 km es el radio aproximado de la tierra
Este ejercicio nos aproxima el radio de la tierra con un margen muy pequeño.
Eratóstenes nació en Cirene en el año 276 a. C y se cree que era de origen caldeo. Fue matemático, astrónomo y geógrafo. Alrededor del año 255 a. C ,fue nombrado director de la Biblioteca de Alejandría por el rey Ptolomeo Evegetes. Trabajó con problemas de matemáticas, como la duplicación del cubo y los números primos. Hemos podido conocer algo de sus trabajos, merced a comentarios y citas de otros autores. Una de sus principales contribuciones a la ciencia y a la astronomía fue su trabajo sobre la medición de la Tierra, para hallar el radio de la tierra solo necesitó dos palos, una buena cabeza y mucha curiosidad. En esta práctica hemos intentado seguir su procedimiento lo mas fielmente posible, pero cn la ayuda de haber leido el libro anteriormente.
Procedimiento
Este ejercicio lo realizaremos sobre una superficie plana, ya que sin ella este ejercicio no se podria hacer, lo que hay que hacer es poner el papel en la dirección donde sale el sol y en donde se pone el sol (este- oeste). Colocaremos un gnomon, es decir una especie de obelisco y cada media hora tomaremos la medida de la sombra que proyecta. Observamos que a las 12 de la mañana es cuando el sol da una iluminacion mayor por lo tanto la sombra adquirirá el mayor tamaño posible, si seguimos avanzando en el tiempo veremos que despues del momento álcido de luz, el tamaño de la sombra disminuye poco a poco. Digamos que las distancias frente al tiempo dentro de una gráfica sería una parábola.
Para tomar como referencia dos puntos tomaremos Madrid y Jaén, la distancia entre ellas es de 335 km, en Madrid al mediodía el sol tenía un ángulo de 48´09 grados y en Jaén tenía un ángulo de 52 ´25grados. Lo que hizo eratostenes fue restar los dos angulos para poder hallar el ángulo que había entre las dos ciudades tomando como centro el centro de la tierra.
52´25-48´09= 4´16 grados entre las dos ciudades tomando como referencia el centro de la tierra.
El siguiente paso es medir el perímetro de la tierra para lo que utilizó una simple regla de tres.
Si en 4´16 grados la distancia es de 335 km en 360 grados la distancia sera x.
Perímetro=360x 335/4’16 = 32860´66 km es el radio de la tierra
Radio=32860´66/ 2x3,14 = 5318´93 km es el radio aproximado de la tierra
Este ejercicio nos aproxima el radio de la tierra con un margen muy pequeño.
Realizado por:
Beltrán de Zavala
Lucas Férnandez
Daniel Salas
